Following interpolation of the DEM, or importing of the DEM from an external application, flat and pit pixels must be treated to ensure flow connectivity. Flat or pit pixels will cause the flow mapping algorithm to fail, hence these pixels and all pixels that flow into them will not be accumulated into the subcatchment that they should realistically drain to. Consequently, the subcatchment delineation will exhibit holes, which will adversely affect the calculation of subcatchment areas and geo-statistics. Imported DEMs may also exhibit pit or flat pixels for a variety of reasons depending on the source of the raster data but most will be found in areas where the topographic relief is small compared with the vertical definition of the sampling technique.
CatchmentSIM includes two algorithms for removal of flat and pit pixels in a DEM. The first of these is a filling algorithm which raises the elevation of flat and pit pixels in an iterative manner until flow processing is possible. The second algorithm for removal of flat and pit pixels is an advanced breaching algorithm based on Priority First Search (PFS) weighted graph methodology.
In the case of internally interpolated DEMs it is recommended that the filling algorithm is initially applied to remove the bulk of the flat and pit pixels and treat the flattened hill crests that tend to result from the DEM interpolation algorithm. Following this, the breaching algorithm may be applied to remove the remainder of the flat and pit pixels.
Where a DEM has been imported from an external application, the breaching algorithm may be applied without prior application of the filling algorithm, particularly if the flat and pit pixels are in valley areas or situated along expected watercourse alignments.
Hydrologic conditioning of DEMs is a key challenge for undertaking hydrologic terrain analysis and is further described in the Key Challenges section.
CatchmentSIM's filling algorithm (DEM Conditioning >> Filling Algorithm) works by first raising all pit pixels to the elevation of their lowest neighbouring pixel and then raising the elevation of flat pixels by a set increment in order to be able to derive a downslope flow direction.
This algorithm is specifically designed to treat drainage anomalies resulting from the flattening of hill crests within the DEM where contour definition has not been provided at the crest of a hill. This occurs because all rays of the interpolation algorithm will find the same contour value, as illustrated in Figure 13.
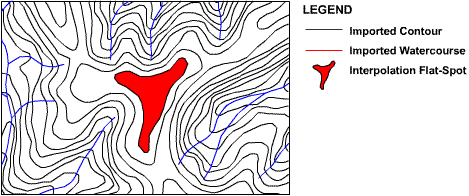
Figure 13 : Interpolation Flat-Spots
In these situations the iterative process implemented by the filling algorithm ensures that pixel elevations in large flat areas are raised from the outside in, creating a rounded hill crest that realistically distributes flow down all sides, with the highest elevation pixel located at the hill crest centroid as shown in the following animation.
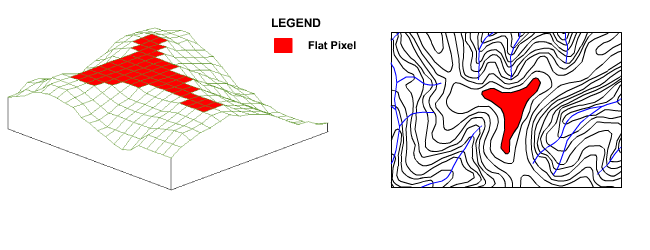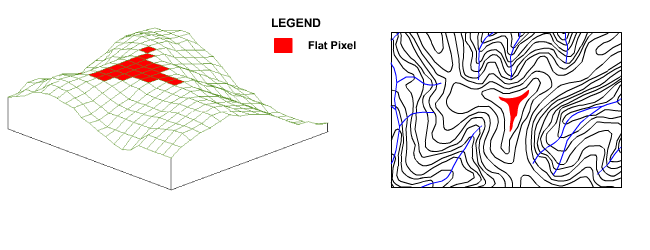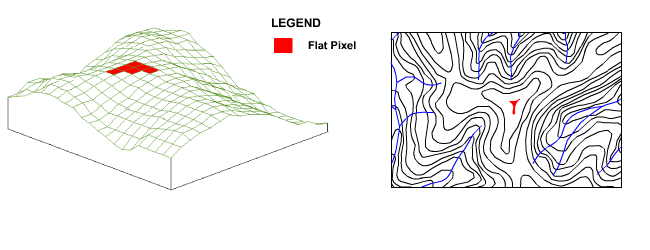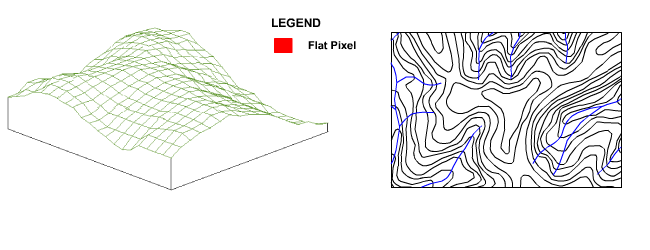
Figure 14 : Effect of Filling Algorithm on Hill Crests
CatchmentSIM's filling algorithm is good at treating drainage anomalies formed in DEMs interpolated internally or by other ray based approaches. However, for imported remotely-sampled DEMs or stubborn flat or pit pixel arrangements that are unable to be resolved by the filling algorithm, an advanced Priority First Search (breaching) weighted graphed based breaching algorithm has been included in CatchmentSIM.
Breaching (Priority First Search) Algorithm
The breaching algorithm implemented within CatchmentSIM is designed to solve complex arrangements of flat and pit pixels in a DEM. The algorithm can resolve any flat or pit pixel within a DEM provided a pixel with a lower elevation exists somewhere within the DEM (subject to minimum downslope gradient criteria). For each flat or pit pixel, the breaching algorithm searches for a nearby pixel with lower elevation (outlet pixel) and an optimum drainage path between the two pixels. After finding the outlet pixel and optimum drainage path, the breaching algorithm will lower the elevation of all pixels along the optimum drainage path to create a downslope drainage path of consistent gradient between the original flat or pit pixel and the outlet pixel.
The method used to implement this technique is based on well-documented weighted graph methodology (Sedgewick, Robert 1988) and has shown promise in hydrologic applications (Jones, Richard 2002). The algorithm records DEM pixels or 'nodes' in two sets, the priority tree and the priority queue. As a result, all pixels in the DEM are in one of three states, on the priority tree, on the priority queue or as yet unseen by the algorithm. Initially, all non-diagonal pixels adjacent to the target flat or pit pixel are added to the priority queue. In turn, the nodes in the priority queue are examined with reference to a priority function and the most suitable node in the priority queue is added to the priority tree and removed from the priority queue. Adjacent pixels to the new node (recently added to the priority tree) are then added to the priority queue which now consists of the remaining nodes from the previous iteration and these new nodes. The algorithm continues until a terminating condition is met, which is triggered when a node in the priority queue satisfies the terminating criteria. In CatchmentSIM, the terminating criteria requires the node to have a lower elevation than the starting node and for the resultant downslope gradient between the two points (along the optimum drainage path) to exceed a user designated minimum gradient threshold.
The priority function used to assess nodes in the priority queue has two criteria. Firstly, it searches for the node representing the smallest net elevation gain from the starting node. If more than one node has an equal net elevation gain then the node representing the shortest path from the starting node (along the optimum drainage path) is selected. This methodology is explained further in Figure 15.
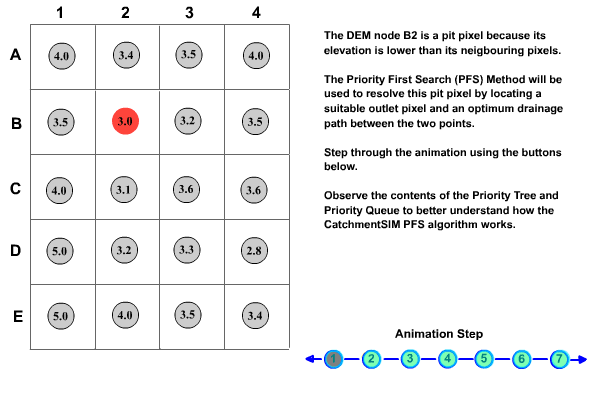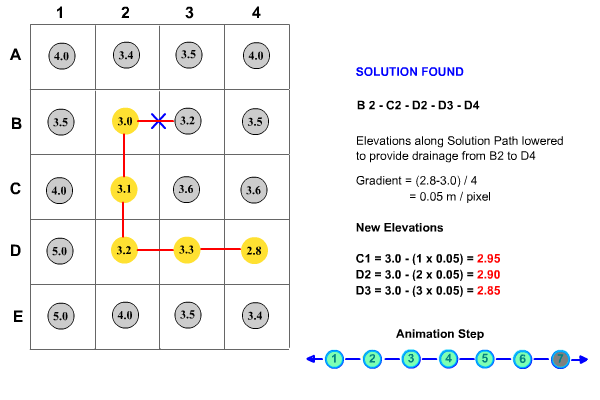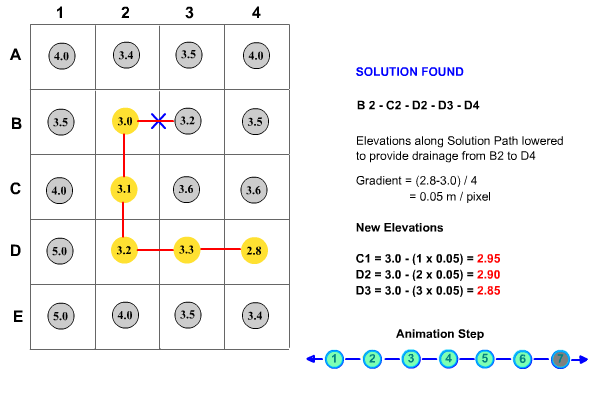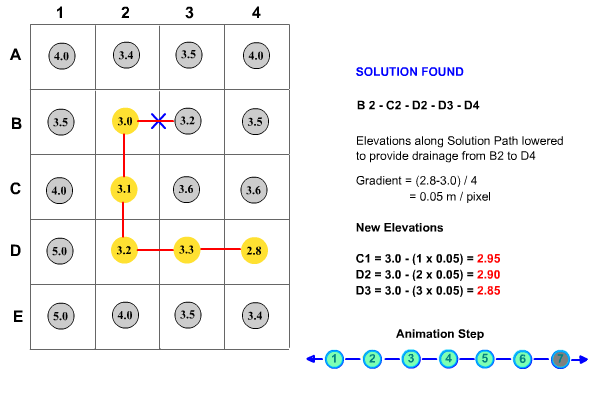
Figure 15 : Priority First Search Algorithm Methodology
One of the important capabilities of the breaching algorithm is that once a node is entered in the priority queue it is not removed until the algorithm is finished or it is transferred to the priority tree. This means that the priority tree can grow in any direction and will always find the optimum drainage path. A real-world example of application of the CatchmentSIM breaching algorithm is shown in Figure 16.
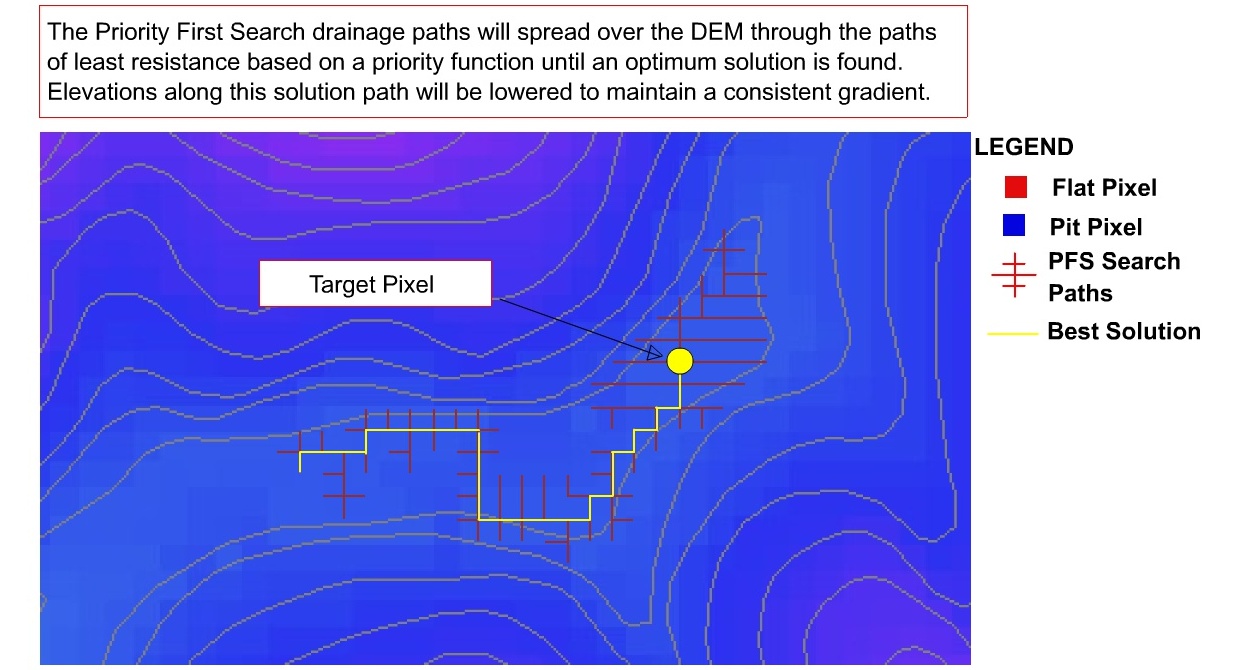
Figure 16 : Sample Animation of breaching Algorithm
The optimum drainage path found by the algorithm in the above example may not seem to be representative of the contours, however it represents the shortest path through the lowest pass over the subtle DEM elevation variations.
The breaching algorithm can be either applied to an individual flat or pit pixel (DEM Conditioning >> Breaching Algorithm >> Process Individual Pixel) by the user or to all flat or pit pixels remaining in the DEM (DEM Conditioning >> Breaching Algorithm >> Process Entire DEM). If the later is applied then the flat and pit pixels are processed by the breaching algorithm in order of increasing elevation. This improves the drainage network in flatter terrain and reduces the necessity for multiple applications of the breaching algorithm.
There are a number of options that a user can set in CatchmentSIM to dictate the properties of the breaching Algorithm (in Project Options form), these are :
•Minimum Gradient – The minimum gradient that must be found to exist along the optimum drainage path for the algorithm to accept the outlet pixel. This parameter is designed to ensure that significant drainage paths are identified and that gradients are not so low as to produce flat pixels when DEM pixel elevations are rounded to the precision of the DEM (single or double).
•No-data Behaviour – This parameter dictates how the algorithm will behave if it encounters pixels which are on the boundaries of the DEM or have not yet been assigned an elevation value. The algorithm can either terminate leaving the original flat or pit pixel with its initial elevation, or continue to search ignoring the no-data or boundary pixel.
•Break Size – This parameter is used to monitor the size of the priority queue and the algorithm will terminate if the priority queue reaches this size. This is particularly important if the no-data behaviour parameter is set to ignore no-data or boundary pixels. In these cases, the algorithm may search the entire DEM before realising that no pixel meets the terminating criteria and moving onto the next flat or pit pixel. This can slow the algorithm down to an impractical extent. To avoid this slow-down and enable the algorithm to terminate prematurely, the breaching break size parameter may be used. This parameter should be set large enough to ensure genuine solutions paths are found but small enough to restrict unwanted algorithm slow-down.
The breaching algorithm has several important advantages over other common methods. Firstly, it is robust and will always find a solution provided a pixel satisfying the terminating conditions exists. Secondly, it does not distinguish between flat and pit pixels resulting in a consistent approach to both types of drainage anomalies. Thirdly, it tends to create channel networks and flow distributions that are more representative of reality than competing algorithms such as the J&D algorithm utilised by ArcGIS and many other software, which tends to create many parallel flow paths (Martz and Garbrecht 1998; Tribe 1992).